Duals
2020 June 14th
Duals
I love when people tell me they want to learn an instrument. Making music is one of my favourite hobbies, but when friends ask for advice I preface it with "there are many ways to play music". The classical pathway was not my approach to learning piano or music theory. Scales and technical exercises were not drilled into me, however I was lucky to be pushed to practice ear training and listening to intervals. For me, I developed musical intuition-based around the space between notes.
Humans hear music very much through intervals - the spacing between two notes. The feeling of two sounds and their relationship to each other is integral to the mood and direction of a melody. Listening to music comes across measured in the distance between notes more so than the naming of pitches (where C to D is a small jump, C to G is a larger jump). Musical scales are defined by their interval patterns regardless of the starting pitch. Similarly, musical rhythm can be intuited by thinking of the time that passes between two notes (again space!).
There are entire schools of musical education that focus on these foundations instead of sheet music and technical precision. Focusing on these spaces — rather than on the specific musical moments full of sound — feels almost counterintuitive. However, this idea is very similar to the principle of mathematical duality which formalizes some ideas of opposing perspectives. We can develop intuition about playing music by looking at it through the opposite lens of space.
Math's Dual Problem
Duality is a concept across a number of mathematical domains. As a theme across these areas, duality allows us to transform a problem, allowing for novel or simpler approaches without changing the nature of the problem.
De Morgan's Laws
De Morgan's laws are common duality principles that are found in logic and discrete mathematics. Our programmer friends (and equally friendly philosophical logicians) have probably seen these laws before. They describe how statements can be related through their opposites.
| Base Statement | Example | Valid when... |
|---|---|---|
not(A) | not(The sky is red) | A is false |
A or B | The sky is red or grass is green | A is true or B is true |
A and B | The sky is blue and grass is green | A is true and B is true |
What happens if we need to negate the statement A or B? These opposites are exactly what De Morgan's laws help us deal with.
| De Morgan's Law | Example | Dual | Valid when... |
|---|---|---|---|
not(A or B) = not(A) and not(B) | not(The sky is red or grass is blue) | not(The sky is red) and not(Grass is blue) | A is false and B is false |
not(A and B) = not(A) or not(B) | not(The sky is green and grass is green) | not(The sky is green) or not(Grass is green) | A is false or B is false |
These duals provide us with an easier problem statement for complex negated statements.
The Optimization Primal and Dual
Dual problems commonly have two perspectives called the primal problem and the dual problem.
My first formal exposure to the idea of duality was in optimization theory. In this example, duals are helpful in solving optimization problems that are not presented in a standard form. Linear optimization is one form of optimization problem whose constraints are linear relationships. The dual of an optimization problem provides a lower bound to the primal problem. If strong duality holds then if the primal for a linear optimization problem has an optimal solution, then the dual also has an optimal solution. This realization (and duality in general) provides us with a method to solve general optimization problems.
Starter problem
We need to purchase materials and where each unit of costs $8 and each unit of costs $40. We also must purchase the materials following certain constraints. We'll also assume that we must purchase positive amounts of these materials.
| Initial Problem | |
|---|---|
| Minimize | |
| Constraints: | |
Minimizing cost in this form is not presented in standard canonical form. In fact, it is the dual for some primal that is in standard form.
Finding the primal
We can produce the primal problem from the dual problem by constructing a matrix using our minimizing function and constraint functions in terms our variables and . We then take the transpose of our matrix by flipping it across its diagonal.
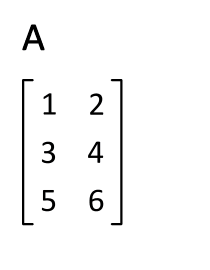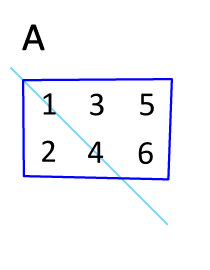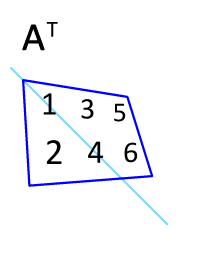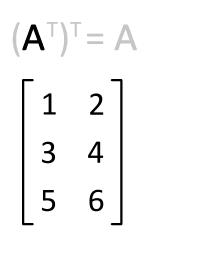
| 3 | 1 | 6 | |
| 1 | 5 | 10 | |
| Minimize | 8 | 40 | 1 |
| 3 | 1 | 8 | |
| 1 | 5 | 40 | |
| Maximize | 6 | 10 | 1 |
We can now turn this into our primal (maximization) problem.
| Primal Problem | |
|---|---|
| Maximize | |
| Constraints: | |
We want our problem in standard form so we can apply the simplex algorithm. It produces a solution of maximizes our primal at $80.
Thanks to the strong duality theorem we know that there exists an optimal solution for the dual (our original problem) with the same optimal value of $80. One solution to minimize our cost is .
Duality in Life
Even in the philosophy of mind we find duality. Mind-body dualism is a view in metaphysics that explores the nature of being human by postulating that the body and mind are two distinct substances. Reflecting on this, we reason about reality with our minds. But, we actually experience reality with our bodies. Which perspective would be the primal and which would be the dual? Although my study of philosophy has been limited, this lends to the pervasiveness of the broad theme of duality. That is to say, duality is a meaningful theme across mathematics but also applied to life in general.
I propose that we actively look for duals when exploring problems in any aspect of our lives. It is a broad paintbrush to add to our toolset and can be a great starting heuristic for outside of the box thinking due to its simplicity (and resultant depth). Start from the opposite, look for our spaces in music, and take time to shift our perspectives.
Thank you for reading. Thank you for exploring ideas with me.

